回复：应用探讨——西门子PID调节应用及技巧探讨-技术论坛-工业支持中心-西门子中国

回复：应用探讨——西门子PID调节应用及技巧探讨

Automann

帖子

6168
精华

138
被关注

308

论坛等级：至圣

注册时间：2004-12-23

普通如何晋级?

发布于 2013-03-16 22:25:12

59楼

quote:以下是引用凌波微步在2013-03-16 20:13:35的发言：

quote:以下是引用Automann在2013-03-15 15:03:32的发言：
单纯的P调节只要增益小，肯定能稳定（没超调），问题是稳态误差与增益成反比，单纯的P调节不能兼顾稳定性和稳态误差。PI或PID可实现超调小和无稳态误差。

我的表述不准确，谢谢廖老师的指正。我已经修改了我相关帖子。

我们来看一下纯比例的公式：M(t)=Kc*ER(t); ER(t)=SP(t)-PV(t)
如果SP不变，Kc不变（我们在实际调节过程中经常使用的方法），那么M(t)与PV(t)就是一个线性关系。
Kc值越大，M(t)越大，输出变化越快。
那么，如果Kc值恰好可以使得PV变化后=SP值，那么M(t)=0，但在实际当中，Kc的值应该是多少，才能是理论上的这个点呢？
考虑到PID调节输出的精度，调节阀门或变频器等设备的控制精度，我们很难找到这个准确的Kc值。即使找到理论上的Kc值，可能由于精度过高，而无法与控制设备的精度相匹配，也很难达到精确到位。
如果Kc太小，那么调节效果如何？------缓慢，作用效果不明显。
如果Kc太大，调节效果如何？-------过快，容易超调，作用效果过强。反而会出现震荡。
---------其实我所说的不稳定，指的就是这种不稳定。我的想法是在Kc有较好的效果的基础上。

不知我的理解是否正确。请廖老师及其他大侠给予指正。

1. “ 如果SP不变，Kc不变（我们在实际调节过程中经常使用的方法），那么M(t)与PV(t)就是一个线性关系。”
这个结论有点问题，比例控制时M(t)和误差成正比，而不是和PV(t)成正比。
2. “如果Kc值恰好可以使得PV变化后=SP值，那么M(t)=0，但在实际当中，Kc的值应该是多少，才能是理论上的这个点呢？”
如果闭环中没有积分环节（即控制理论中的0型系统），稳态误差和开环增益成反比。要想PV=SP（误差为0），增益应为无穷大，显然是不可能的。换句话说，纯比例控制不能消除稳态误差，所以要用PI代替比例控制。
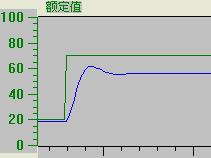
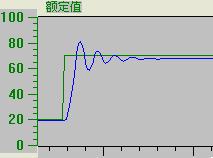
下面的两个图都是比例控制，一个增益小，较平稳、稳态误差大，第二个增益大，波动较大、稳态误差小。